|
DirectXGraphics:
Smooth Keyframe Animations
Author:
Jack Hoxley
Written: 4th September 2001
Contact: [EMail]
Download: GR_SmoothAnim.Zip
(1061kb)
Contents
of this lesson
1. Introduction
2. About the function(s)
3. Application of the function
1.
Introduction
Welcome
to another extended tutorial for Direct3D8 programming
in visual basic. For todays article we'll be covering
smooth keyframe animation. This builds directly
upon the code, and the technique learnt in the
previous lesson in this series - number 10 (read
it here). If you
haven't read it, read it first - otherwise you'll
be lost here!
2.
About the function(s)
The
functions that we're going to use are fairly standard
maths algorithms, and they do look pretty ugly!
but exactly how they work is really not at all
important here (I have no idea how to derive such
parametric equations), all you need to know is
what they do, and how to use them.
I'm
going to examine 3 types of function - there is
a fourth, the Bezier curve, but whilst it's better
known and looks slightly nicer it's absolutely
useless for animation as the curve has a nice
tendency to do absolutely different things to
the animation!
Type
1: Standard Linear Equation
this is the standard equation that we've
used before (in lesson 10). The maths equation
looks like this:
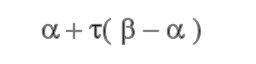
where:
a = Source point
(x,y)
b = Destination
point (x,y)
t = Interpolant
between 0.0 and 1.0, at t=0.0 we get point
a, and at t=1.0 we get point b, at t=0.5
we get a value 1/2 way between the two.
this
produces a keyframe animation between 5 points
that looks like this:
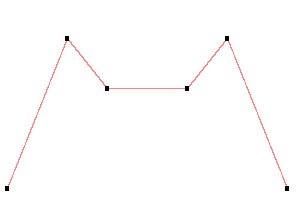
looks
good enough, if the black dots are our keyframes
then any frame between those will be somewhere
on the red line. The big draw back here is the
asphetic appearance of the whole thing - take
the 2nd and 5th keyframes, they result in rather
significant changes of direction, on screen this
can look a little odd - your character may appear
to jerk their legs/arms in a completely different
direction...
Type
2: Hermite Spline Equation
So we solve the previous problem with a new
function. This is where it gets more interesting,
instead of suddenly changing direction at the
keyframes it slowly (or quickly) blends between
the new and old direction - producing a nice,
rounded, smooth line going through all the keyframes...
The
maths equation for this is complicated - and it
looks ugly! Just check this one out:
Looks
pretty dont it! And all those parameters mean:
t = interpolation
amount, 0.0 to 1.0 - same as for linear function,
0.0=start and 1.0=end
P0 = Start point
P1 = End point
M0 = Tangent at start
M1 = Tangent at end
The
second equation is used to calculate the tangents
M0 and M1, and is fairly simple really.
a = tensile factor, 0.0 = Smooth curve, 1.0 =
straight line, -1.0 = very bendy line!
Stick
this all together and we get a curve looking like
the one in the following diagram - using the same
keypoints as the linear example, you can see how
much smoother the result is.
Type
3: Catmull-Rom Splines
This is the last type we're going to look
at, and to all intents and purposes it's a simpler
version of the hermite spline formula - and for
a=0.0 you tend to get
an exactly identical result. It is also slightly
faster to compute:
Still
quite complicated, but really not that bad when
it comes to using it.
t = Interpolant
amount, again, on a 0.0 to 1.0 scale
P0 = First point
P1 = Second point
P2 = Third point
P3 = Fourth point
the
equation actually only draws a curve between points
P1 and P2, it uses P0 and P3 to guide the curve
(so it know where the curve should go basically).
The end result looks like this:
3.
Application of the function(s)
All
of the source code for this is included in the
download, so you'll need to get that in order
to see how it all fits together. It's essentially
been built around the download for lesson #10
- the original keyframe tutorial. The only major
difference being that there are some additional
functions for interpolating using the different
methods.
You
should of already worked out that the two new
functions are going to be slower than the basic
linear equation, but thats the trade off between
performance and presentation... to help combat
this I've included my own custom C++ DLL to do
some of the grunt work, and it does do it considerably
quicker (200fps instead of 80fps), you can use
this library if you really want to - or you can
use straight VB code, your choice entirely.
Another
possibility is the application to skeletal animation
with this sample, you can use these functions
to interpolate the bones more smoothly - if they
are currently setup on a keyframe system.
I
strongly suggest that you download the sample
code and watch the animation run through a few
times in each mode (tap SPACE to change), I found
it very easy to tell between the spline and the
linear functions - you can even notice the triangles
changing shape with the linear function (not good).
Also, many thanks to Dmitriy Safro (www.safrosoft.com)
for providing the 3D model.
You
can download the source code from the top of the
page, or from the downloads
page. enjoy...
any
feedback or improvements can be emailed to me
- I'm always interested...
|

