DirectXGraphics: Billboarding
Author: Jack Hoxley
Written: 25th May 2001
Contact: [EMail]
Download: Graph_15.Zip (181kb)

Contents of this lesson
1. Introduction
2. The maths behind it all
3. Migrating this into D3D

1. Introduction

Welcome back for another lesson in the world of Direct3D graphics. In this lesson we'll learn how to build cutting edge graphics into our games - without requiring a super computer. Before you get excited though, this isn't quite the answer to everything - it only works in certain cases, and doesn't always look perfect - but it's a commonly used technique in commercial games, so there's no reason to avoid it.

When you play any action game on the PC your almost guaranteed to see an explosion at some point - sometimes they are breathtaking, other times they are fairly lame excuses for explosions - either way, with the techniques and skills you've learnt in this series you'll be aware that something clever must be happening. The only way we've learnt so far to replicate an explosion is to use the particle effects (point sprites), but you'll also be aware that your limited to the number that can be rendered - a decent explosion would require 1000's if not millions of these particles - very slow using these methods. So how do they do it, if they're not using raw geometry?

The answer is very simple, and in truth it's just a visual trick - after reading this article, if you go back and play unreal tournament, Deus Ex, Half Life (or whatever takes your fancy) you may be able to catch them at it. The explosion itself is just a clever use of animation, textures and a little bit of geometry; one of the artists has used a program to render an explosion onto a series of textures, and the programmer uses these textures, a few triangles and some alpha blending to put it in the game engine. The original explosion textures could take 3 days to render for all we care - once they're rendered we can use them in our game just the same as any other texture.

(Thanks to Xtreme Game LLC)

Above is an example of the animations I'm talking about, you can see that straight away it would be very very difficult to replicate something like that on-the-fly, and doing it fast would be even harder! The visual trick behind all of this is called billboarding. In our 3D world we orientate 2 triangles in the form of a square so that they exactly face the camera; this means that they appear with the correct aspect ratio and perspective, yet they can still be scaled and occluded by other aspects of our 3D world (distance for example).

2. The maths behind it all

The maths involved is simply down to working out the correct angle that we want to rotate the billboard by, in some worlds this can be extremely simple - just around the Y axis, whereas others will need to be rotated around all 3 axis; on the other hand, you may well not want them rotated around a particular axis because it'll look wrong - take a tree for example, you don't want it to rotate so that the trunk/roots appear to come out of the ground...

Before we get started here credit is due to Eric Coleman who pretty much wrote all of the proper billboarding maths and code - thanks to him! You can see what he's working on here: Gladiator - Fields Of Slaughter. The following steps are an adapted version of what Eric explained to me via email and a sample program...

The problem: To rotate a simple quad (2 triangles) so that it faces the camera:

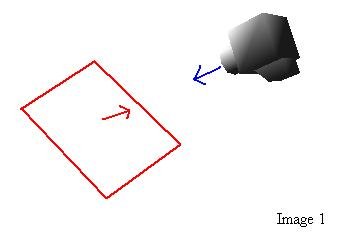
Step 1: Calculate the direction vector:
Maths: vN = -vTo + vFrom
In VB:

vN.X = -vTo.X + vFrom.X
vN.Y = -vTo.Y + vFrom.Y
vN.Z = -vTo.Z + vFrom.Z

Step 2: Convert To Spherical Coordinates
We now have a direction vector, which if placed at the origin can be treated as a point in 3D Space, as shown in the following diagram:

We want to change this point into spherical coordinates, which can be done using the following maths:

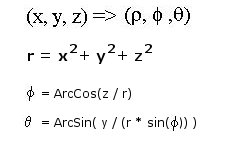
And all this in VB is:

R = Sqr(vN.X * vN.X + vN.Y * vN.Y + vN.Z * vN.Z)
                                                          
temp = vN.Z / R
If temp = 1 Then
    BBphi = 0
ElseIf temp = -1 Then
    BBphi = PI
Else
    BBphi = Atn(-temp / Sqr(-temp * temp + 1)) + (PI / 2)
End If
                                                          
temp = vN.X / (R * Sin(BBphi))
If temp = 1 Then
    BBtheta = 0
ElseIf temp = -1 Then
    BBtheta = PI
Else
    BBtheta = Atn(-temp / Sqr(Abs(-temp * temp + 1))) + (PI / 2)
End If
                                                          
If vN.Y < 0 Then
    BBtheta = -BBtheta
End If

This next image shows the relationship of phi and theta - the two angles that we just found while converting to spherical coordinates...

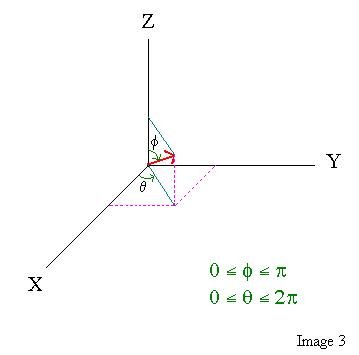
Step 3: Rotating
We now know the angles by which we need to rotate the billboard, all we need to do is actually rotate them...
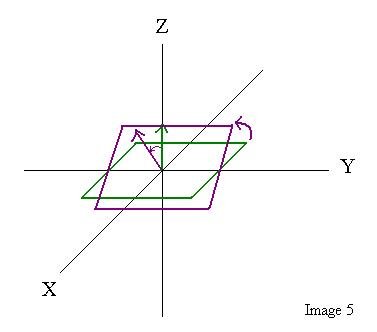
First we start off with the plain geometry; this must be created in the XY plane - as demonstrated by the next diagram:

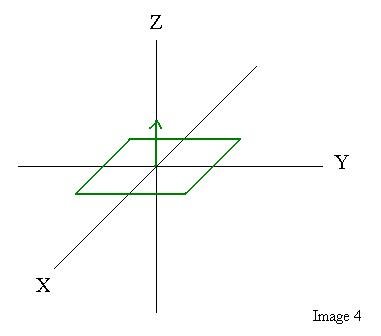
The first step to rotating the billboard is to rotate it phi radians around the Y axis, in maths this will look like this:

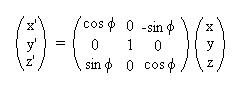
Graphically it looks like this:

and in VB this will be:

x = V.x * cos(phi) - V.z * sin(phi)
z = V.x * sin(phi) + V.z * cos(phi)
V.x = x
V.z = z

The next step is to rotate around the Z axis by theta radians. Graphically this will be:

and mathematically:

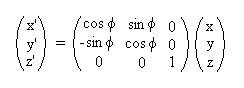
finally, in VB this looks like

x = V.x * cos(theta) + V.y * sin(theta)
y = -V.x * sin(theta) + V.y * cos(theta)
V.x = x
V.y = y

The final step is to translate the billboard back to it's original coordinates - a simple vector addition.

Conclusion
Right, above is all you need to know to construct the relevent rotations for a billboard - but it isn't the end of the world if you dont completely understand all the maths behind it - the following D3D code implementation should be enough for most people.

3. Migrating this to Direct3D

Now that we have the mathematics worked out, we need to make this work with code...

We're going to break this into two main sections - cheap billboards and proper billboards, the former is a simple method that I came up that doesn't rely on any maths; the latter is the implementation of Eric Coleman's maths for rotating the geometry. Cheap billboards are functional and can be set up easily in about 2 minutes, but aren't really useful when you can do proper billboarding - but I thought I'd leave them in here, should you really want to use them...

A: Cheap Billboards
This method uses transformed and lit vertices - you transform the billboard coordinates into screen space, then draw a quad (2 triangles in a square shape) around the coordinate - simple really. It's effectively the same as the point sprites demonstrated in this previous tutorial. Here's the following code that makes it all work (taken from the sample application):

Private Sub RenderCheapBillboards(vp As D3DVIEWPORT8)
'######################
'## 0. DECLARATIONS ##
'#####################
    Dim I As Long, X As Long, Y As Long
    
    Dim v2D(0 To 4) As D3DVECTOR, Verts(0 To 3) As TLVertex
    Dim Ref(0 To 4) As Long 'sort the depths...
    Dim Depths(0 To 4) As Single
    '   - NB: wont respond to camera roll.
    
    '##########################
    '## 1. SETUP THE DEVICE ##
    '########################
    
    D3DXMatrixIdentity matWorld
    D3DDevice.SetRenderState D3DRS_ALPHATESTENABLE, 1 'alpha testing is useful... ;)
    D3DDevice.SetRenderState D3DRS_ALPHAFUNC, D3DCMP_GREATEREQUAL 'Pixel passes if (pxAlpha>=ALPHAREF)
    D3DDevice.SetRenderState D3DRS_ALPHAREF, 50 'only if the pixels alpha is greater than 
                            'or equal to 50 will it be rendered (skips lots of rendering!)
    D3DDevice.SetRenderState D3DRS_ZWRITEENABLE, 0 'we dont want to affect the depth buffer
    D3DDevice.SetTexture 0, TexExplosion
    D3DDevice.SetVertexShader FVF_TLV
        
    '######################################
    '## 2. TRANSFORM TO SCREEN SPACE ##
    '####################################
    For I = 0 To 4
        D3DXVec3Project v2D(I), ExpTranslate(I), vp, matProj, matView, matWorld
        Ref(I) = I
        Depths(I) = v2D(I).Z
    Next I
    
    '#####################
    '## 3. SORT DEPTHS ##
    '###################
        Dim Changes As Long, tmp As Single, lTmp As Long
        Changes = 1 'just to get it started...
        Do While Changes > 0
            Changes = 0
            For I = 0 To 3
                If Depths(I + 1) > Depths(I) Then
                     tmp = Depths(I)
                     Depths(I) = Depths(I + 1)
                     Depths(I + 1) = tmp
                     lTmp = Ref(I)
                     Ref(I) = Ref(I + 1)
                     Ref(I + 1) = lTmp
                     Changes = Changes + 1
                End If
            Next I
        Loop
    
    '###########################
    '## 4. RENDER THE QUADS ##
    '#########################
    For I = 0 To 4
            '//Generate the vertices.
            Verts(0) = CreateTLV(v2D(Ref(I)).X - 100, v2D(Ref(I)).Y - 100, v2D(Ref(I)).Z, _
                                 _ 1, &HFFFFFF, 0, 0)
            Verts(1) = CreateTLV(v2D(Ref(I)).X + 100, v2D(Ref(I)).Y - 100, v2D(Ref(I)).Z, _
                                 _ 1, &HFFFFFF, 1, 0)
            Verts(2) = CreateTLV(v2D(Ref(I)).X - 100, v2D(Ref(I)).Y + 100, v2D(Ref(I)).Z, _
                                 _ 1, &HFFFFFF, 0, 1)
            Verts(3) = CreateTLV(v2D(Ref(I)).X + 100, v2D(Ref(I)).Y + 100, v2D(Ref(I)).Z, _
                                 _ 1, &HFFFFFF, 1, 1)
            
            X = ExpFrame(Ref(I)) Mod 4
            Y = ExpFrame(Ref(I)) \ 4
            
            '//Set up the correct texture coordinates
            Verts(0).T.X = X / 4: Verts(0).T.Y = Y / 4
            Verts(1).T.X = (X + 1) / 4: Verts(1).T.Y = Y / 4
            Verts(2).T.X = X / 4: Verts(2).T.Y = (Y + 1) / 4
            Verts(3).T.X = (X + 1) / 4: Verts(3).T.Y = (Y + 1) / 4
            
            '//Update the current frame if necessary
            If GetTickCount - ExpLastChange(I) > ExpSpeed(I) Then
                ExpLastChange(I) = GetTickCount
                ExpFrame(I) = ExpFrame(I) + 1
                If ExpFrame(I) > 11 Then ExpFrame(I) = 0
            End If
            
            '//Finally, render the quad
            D3DDevice.DrawPrimitiveUP D3DPT_TRIANGLESTRIP, 2, Verts(0), Len(Verts(0))
    Next I
    
    '#############################
    '## 5. CLEAN UP THE DEVICE ##
    '###########################
    D3DDevice.SetRenderState D3DRS_ALPHATESTENABLE, 0
    D3DDevice.SetRenderState D3DRS_ZWRITEENABLE, 1  'we dont want to affect the depth buffer
End Sub

right, that shouldn't look too nasty :)
Basically, we collect the depth values for all the billboards, as well as the 2D coordinate that they'll be rendered to. We then sort out the Ref( ) array to point, in order, to the deepest-closest before rendering them. Why do this? Because we're alpha blending the sprites - alpha blending is dependant on the current pixels rendered behind it - so if you draw them in any order you'll get some strange artifacts, so we sort them, then draw the deepest before the shallowest so that we dont get any artifacts. The only two drawbacks with this method is that the billboards dont respond to the roll parameter in the projection matrix setup (so if the rest of the world rolls over the billboards wont), also there may well end up being some depth related issues - whilst they should be rendered at the correct depth, there is a slight possibility that they'll get out of sync towards the end of the depth buffer range (1.0) - this is a property of Z-Buffers and cant be worked around.

B: Proper Billboards
Okay, now onto the more complicated method, the one that Eric designed, and the one with all the maths... :)

We're going to set up two main functions, one to calculate the required angles - this must be called on every update of the camera; and another function to construct the relevent matrix for the billboards - this must be called for every billboard. Finally there is a sub routine that uses the results of these two master functions to render the final product.

First up, the function for calculating the angles, some of the code here may look familiar:

Public Sub FindAngles(vFrom As D3DVECTOR, vTo As D3DVECTOR)
'//Finds the angles required to set up the correct
'//billboard rotations. Written by Eric Coleman (thanks!)
                                                          
Dim vN As D3DVECTOR
Dim R As Single, temp As Single
'//1. Calc. Vector from Cam->BBoard
vN.X = -vTo.X + vFrom.X
vN.Y = -vTo.Y + vFrom.Y
vN.Z = -vTo.Z + vFrom.Z

'//2. Convert to spherical Coords
R = Sqr(vN.X * vN.X + vN.Y * vN.Y + vN.Z * vN.Z)

temp = vN.Z / R
If temp = 1 Then
    BBphi = 0
ElseIf temp = -1 Then
    BBphi = PI
Else
    BBphi = Atn(-temp / Sqr(-temp * temp + 1)) + (PI / 2)
End If

temp = vN.X / (R * Sin(BBphi))
If temp = 1 Then
    BBtheta = 0
ElseIf temp = -1 Then
    BBtheta = PI
Else
    BBtheta = Atn(-temp / Sqr(Abs(-temp * temp + 1))) + (PI / 2)
End If

If vN.Y < 0 Then
    BBtheta = -BBtheta
End If
                                                          
End Sub

Private Sub GenerateBBMatrix(Index As Long)
Dim tempMatrix As D3DMATRIX
Dim tempMatrix2 As D3DMATRIX

Finally we have the wrapper sub, the one that controls everything! This may require some explanation though. It's divided into 6 nice sections for you - which makes things nice and easy. The first and the last section configure the device, the only important parts here are the alpha testing and Z-Writing; firstly I've set it up to not render any pixels with an alpha value of less than 50 (of 255) - the sample code uses alpha maps (as demonstrated in this previous tutorial) and alpha testing is an interesting little feature I thought I may as well include. Secondly there is the Z writing, which I disable at the start of the sub and enable again at the end - the billboards aren't really 'there' in this case, so I dont want them to affect other geometry (if Z writing was enabled anything behind them would not get rendered if the billboard has already been rendered). Also, we're using a simple sorting algorithm (bubble sort to be precise) so that we render the billboards back-front in world space - this is purely for alpha blending purposes; if you're not using any form of alpha blending then you can skip this part. Alpha blending is draw depth dependent, which is why this is necessary.

Private Sub RenderProperBillBoards(vp As D3DVIEWPORT8)
Dim I As Long, X As Long, Y As Long
Dim StoredMatrices(0 To 4) As D3DMATRIX '//we need to cache the matrices...
Dim Depth(0 To 4) As Single, vTmp As D3DVECTOR
Dim Ref(0 To 4) As Long 'pointer to correct value...
                                                          
'#########################
'## 1: SETUP THE DEVICE ##
'########################

D3DDevice.SetVertexShader FVF_LV
D3DDevice.SetTexture 0, TexExplosion
D3DDevice.SetRenderState D3DRS_ALPHATESTENABLE, 1 'alpha testing is useful... ;)
D3DDevice.SetRenderState D3DRS_ALPHAFUNC, D3DCMP_GREATEREQUAL 'Pixel passes if (pxAlpha>=ALPHAREF)
D3DDevice.SetRenderState D3DRS_ALPHAREF, 50 
D3DDevice.SetRenderState D3DRS_ZWRITEENABLE, 0 'we dont want to affect the depth buffer
'####################################
'## 2: CALCULATE NECESSARY DATA ##
'###################################

For I = 0 To 4
    X = ExpFrame(I) Mod 4
    Y = ExpFrame(I) \ 4

    '//Set up the correct texture coordinates
    Exp(I).V(0).T.X = X / 4: Exp(I).V(0).T.Y = Y / 4
    Exp(I).V(1).T.X = (X + 1) / 4: Exp(I).V(1).T.Y = Y / 4
    Exp(I).V(2).T.X = X / 4: Exp(I).V(2).T.Y = (Y + 1) / 4
    Exp(I).V(3).T.X = (X + 1) / 4: Exp(I).V(3).T.Y = (Y + 1) / 4

    '//Update the current frame if necessary...
    If GetTickCount - ExpLastChange(I) > ExpSpeed(I) Then
        ExpLastChange(I) = GetTickCount
        ExpFrame(I) = ExpFrame(I) + 1
        If ExpFrame(I) > 11 Then ExpFrame(I) = 0
    End If

    '//Calculate the correct rotation/translation matrix for the geometry
    GenerateBBMatrix I
    StoredMatrices(I) = matWorld 'cache this matrix for usage later on. 
    NB: it is the currently set matrix though...
Next I

'##########################################
'## 3: GATHER PROJECTED DEPTH VALUES ##
'########################################
For I = 0 To 4
    D3DXVec3Project vTmp, ExpTranslate(I), vp, matProj, matView, matWorld
    Ref(I) = I
    Depth(I) = vTmp.Z 'all we want is the Depth-Buffer value.
Next I

'###########################
'## 4: SORT DEPTH VALUES ##
'##########################

Dim Changes As Long, tmp As Single, lTmp As Long
Changes = 1 'just to get it started...
Do While Changes > 0
    Changes = 0

    For I = 0 To 3
        If Depth(I + 1) > Depth(I) Then
            tmp = Depth(I)
            Depth(I) = Depth(I + 1)
            Depth(I + 1) = tmp
            lTmp = Ref(I)
            Ref(I) = Ref(I + 1)
            Ref(I + 1) = lTmp
            Changes = Changes + 1
        End If
    Next I

Loop

                                                            

                                                            

'#############################################
'## 5: RENDER DEEPEST FIRST-CLOSEST LAST ##
'############################################
For I = 0 To 4
    D3DDevice.SetTransform D3DTS_WORLD, StoredMatrices(Ref(I))
    D3DDevice.DrawPrimitiveUP D3DPT_TRIANGLESTRIP, 2, Exp(Ref(I)).V(0), Len(Exp(Ref(I)).V(0))
Next I



'###########################
'## 6: TIDY UP THE DEVICE ##
'#########################
D3DDevice.SetRenderState D3DRS_ALPHATESTENABLE, 0
D3DDevice.SetRenderState D3DRS_ZWRITEENABLE, 1

End Sub

Well, there we have it - another tutorial down. Hopefully you'll find this technique useful in the future... go play some of the top 3D action games and I'm pretty sure you'll notice some nice billboard-based special effects in action...

I strongly suggest that you download the complete source code for this tutorial. After that, you can move onto the next tutorial - Lesson 16 : Visibility Testing and Culling to increase speed