Visibility Testing
Author : Jack Hoxley
Written : 14th March 2001
Contact : [Web] [Email]
Download : Graph_16.Zip [16 Kb]

Contents of this lesson:
1. Introduction
2. Vector Based Culling
3. Frustum Culling
4. Projection/Bounding Box Culling
5. Tips and Tricks

1. Introduction

By this point in the series you should be getting fairly familiar with 3D programming and the Direct3D interfaces; the chances are that you've also started your own little project, or begun thinking about it (if you like 3D that is). This section of "useful techniques" are articles that explain things that aren't necessarily part of Direct3D or it's interfaces, but may well be required when using them - or are made easier using them. Many of these tricks use the D3DX libraries maths functions to simplify things, but where relevent the actual technique behind them will be explained.

The first useful technique I want to cover is that of visibility testing. Someone once said (I dont know who): "The fastest polygons are the ones you dont draw", this should make perfect sense, we only have a finite amount of power to play with, and when you want your game to run at any sort of reasonable pace you'll always be juggling between what you can do and what you want to do. Despite the ever increasing power that 3D cards are providing we dont want to waste any time or resources that we dont need to, the simplest way is to reduce the number of objects or vertices that we are being sent to render. Whilst Direct3D will clip geometry to fit the screen it still does quite a lot of processing on hidden and/or offscreen geometry - geometry that it is quite likely the player will never see. To stop Direct3D wasting valuable time programmers employ a handful of tricks and algorithms to determine whether or not geometry should be rendered (based on it being on/off screen).

There are 100's of different methods for doing this, different ones will suit different worlds/game types - its up to you to choose the one you like the most or design a custom version based on multiple different methods. This article covers 3 types of culling (removal of geometry we dont want) methods, and then offers some tips and tricks for using these algorithms.

2. Vector Based Culling

This first method is an extremely simple one, and was designed by myself for use with "3D-World" (the final piece for this series), it may well have been documented and used before, but I didn't read up on it before hand. The major flaw with this algorithm is that it only suits very specific environments, landscapes particularly - buildings/indoors scenes as well, but other engine types will not always work so well using this technique.

The basis of this technique is the usage of a common 3D graphics formula, the Dot Product - this is covered again in Useful Techniques number 2, so I'll only skim through it here. The dot product of two vectors (that are normalised) will give us a value representative of the angle between them (The cosine to be precise). We can use this value to tell if a point is in front of the camera, and within a given degree of the camera's direction.

U•V = (U.X * V.X) + (U.Y * V.Y) + (U.Z * V.Z)
U•V = (U.X * V.X) + (U.Y * V.Y)

The Dot product formula for 3D vectors (top), and 2D vectors (Bottom). If the vectors are normalised (a length of 1) then the result will lie between -1 and +1. If we take the vector U to be the direction that the camera is facing (calculated using the Unit Circle Theorem) and V to be the vector from the camera to the point in question, we can calculate the angle, which will give us the results depicted below. Currently it's only in 2D, but that's partly because it's easier to show as a diagram.

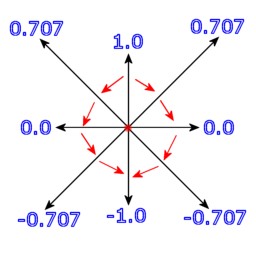
All of the above vectors (represented by black lines) are compared with a vector going straight up - [0,1], a vector going the same direction gets a result of 1.0 - as shown, a vector going perpendicular to [0,1] will get a result of 0.0, and any vector between will get a value between 0.0 and 1.0. Any vector going in a direction away from [0,1] will get a negative value - also shown on the diagram.

Using this information it is going to be quite simple to construct a test that rejects any points that are behind it, or out of range given a reference value. When setting up your projection matrix you will have specified a FOV angle (usually in radians), if we convert this angle to a vector we can say any comparisons with a result less than this is NOT in view, and any comparisons with a result greater than this IS in view. To calculate the comparison value we can use a simple bit of trig maths - this can be done on paper before hand, once you have the values you can store them as a CONST value and use them forever after - they wont change. The most commonly used angles are 45, 60 and 90 degrees, the following diagram illustrates how we can work the dot product reference value out. If we take the view cone as a 2D triangle, where the known angle is half of the total view angle (two triangles will make up the whole cone), we can take a two known distances and either use trig to find the third, or use pythagorus's theorem:

The above triangles represent 45, 60 and 90 degree view angles, for simplicity I'm making the adjacent = to 1, and we want to find the opposite (labelled ?) - we will then have a 2D coordinate for the outer corner (not the 90 degree one) proportional to the origin (which is where the corner with the angle is). We can then normalise this vector, and then compare it with the vector for the adjacent, [1,0] to get the value we want. Here we go:

The length ?'d, using inverse tan will be:

45 Degree cone
Tan(22.5) = ? / 1
? = Tan(22.5)
? = 0.4142135624

60 Degree cone
Tan(30) = ? / 1
? = Tan(30)
? = 0.5773502692

90 Degree cone
Tan(45) = ? / 1
? = Tan(45)
? = 1

We now know the coordinates of the point:

45 Degrees : [1, 0.4142135624]
60 Degrees : [1, 0.5773502692]
90 Degrees : [1, 1]

if we normalise these vectors we get the direction from the origin to the point:

45 Degrees : [0.9238795325, 0.3826834324]
60 Degrees : [0.8660254038, 0.5]
90 Degrees : [0.7071067812, 0.7071067812]

If we now perform a 2D Dot product calculation on the adjacent vector ( [1,0] ) and the vectors listed above we'll get our reference value for each view angle, the results are:

45 Degrees : 0.923879325
60 Degrees : 0.8660254038
90 Degrees : 0.7071037812

You may notice that these value are just the X component of original vectors; this is simply because the adjacent vector, [1,0], doesn't alter the X component (multiply by 1) and the Y component is made to be 0 (multiply by 0) - resulting in the X component being the Dot product value.

You can store these values and use them whenever you like without recalculating them, and if you need a different angle you can quite easily re-write the above calculations to compensate. Also note that you may need to allow a little room when doing the culling, the 3D World final piece uses a 45 degree view angle, yet a dot product comparison figure of 0.865 and 0.845 (depending on what it's rendering) - originally it used 0.924, but based on observation it occasionally clipped points that it shouldn't have done - so I kept taking away a little bit until I decided it wasn't elminintating many triangles - it still does sometimes, but compared with the amount of excess triangles it draws I kept it as it is.

So we've come this far, and not a great deal has happened. We need to write some code that uses all these facts and bits of theory - a simple function that will take a set of points and return if it's visible or not.

Not too complicated really, First it gets the direction vector from the camera to the point in question, then it compares this to the vector defined by the angle the camera is pointing (we could also calculate this by using vAt-vEye from the view matrix). Next it performs the dot product calculation, it then takes the result and compares it with the reference value, if it passes it checks the distance, if it's within range then the point is visible - the functions returns true. If it fails it does an additional check where it's more lenient, and only passes it if it's very close to the camera - during testing I found that there were occasional anomalies close to the camera - this little bit of code solved it.

A couple of things to note about the above code:
1) It uses the D3DX library, whilst this is an article about Direct3D you can replace these calls with equivelent functions (should you be using a newer/older version of DirectX, or not using DirectX at all...)
2) It uses the standard GetDist2D() call - this is a simple function that returns the distance between two points in 2D space, and looks like:

3) It uses the unit circle theorem, in this case it just reads from a lookup array of precalculated integer angles (0 to 360), If you haven't seen this before check out the maths article later on. Briefly though - the X and Y components can be calculated like so:

Done!

Using the above function youcan now tell in 2D if a point is within a given angle, if you modify this it will tell you if the point is within a cone defined by the angle. This method is only really useful for landscape or planar worlds - where everything originates from the same (or similiar) height, like the insides of an office/building. When using height mapped worlds (for landscapes), you can test the center of every tile for visibility - the grid the map is based on is 2D (ignoring the Y/height dimension). For a working example of this wait for the (or go see if it's ready) 3D-World final piece.

3. Frustum Culling

Frustum culling is one of the more common techniques used - it's based in full 3D unlike the vector one above, and is fairly simple to implement, whilst not incredibly accurate it usually does the job adequately.

First off, what is the frustum? this is the area of 3D space that is projected onto the screen when you render a scene. It is defined by a series of planes, these planes are then used to reject geometry. The frustum is illustrated using the following diagram:

(My apologies for the appalling diagram!)

In the above diagram, the blue arrow shows where the camera is facing/looking, the smaller square is the near clipping plane (only vertices beyond this are accepted), the larger square is the far clipping plane (only vertices in front of this are accepted), and the 4 sides joining them up are the side clipping planes. the size and shape of this volume are defined by the viewport settings, projection matrix and the view matrix.

What we need to do is construct a set of 6 planes based on this shape, and suited to fit our world settings. The code for this is quite complicated, and is included in the DirectX8 SDK helper libraries, which is where this next piece of code comes from (I didn't write it is what I'm saying!):

looks nasty doesn't it... you dont really need to understand it in order to use it - so dont worry about how it does things. In order to use this code you must have an array of 6 D3DPLANE objects, and you must call this function everytime you change the camera position (not everytime you want to check a points visibility). An example:

the ComputeClipPlanes( ) call uses the same parameters that you have done for your view and projection matrices.

Finally, after we have constructed the information that we need we have to be able to use it. The next piece of code (also from the SDK files) shows us how we can pass a sphere and it'll tell us if it's visible or not:

In order to use this we pass the point in question as the Center parameter, and a radius of your choice as the second. The radius can be very small (0.00001 or something) if you only want to check the point, if you want to check a large area you can increase the radius. If any part of the sphere is visible then the function returns true.

The fact that it returns true for any of the sphere being visible is it's only downfall, but it only means that you need to be a little more careful when you're using the method. If you used an entire sphere for a model, and the model only occupied a small part of the sphere (yet it required a large radius) then you could get the situation where it renders the model - but it's not actually on screen. To solve this you would want to investigate using multiple spheres and correlating the results.

4. Projection/Bounding Box culling

This final method is my current favourite, I first read up on it in the Visual Weather Documentation, having since explored its usage I've decided it's a very easy to use, fast and very accurate as well - just what I like.

What we are trying to achieve with these algorithms is to rule out any unnecessary geometry that wont appear on screen, therefore, if we could find out where a point will be projected from 3D space into 2D space we would be able to tell if it's within the screen boundaries. Fairly simple really. We could then expand this to be using a bounding box method, where we choose a relevent size box that suits the model we're querying - we then work out if any/all of the 8 corners of the cube will be on the sceen, if any of them are then at least part of the model should be visible. If you wanted you could check every major vertex in the model, but for complicated models this would be quite slow - and start to eat away from the speed advantage that we're chasing.

Luckily for us, DirectX8, in the form of the D3DX helper library has a little function that allows us to give a 3D point and recieve the 2D coordinate for where it would be rendered on the frame buffer, it looks like this:

D3DXVec3Project( _ 
    VOut As D3DVECTOR, _ 
    V As D3DVECTOR, _ 
    Viewport As D3DVIEWPORT8, _ 
    Projection As D3DMATRIX, _ 
    View As D3DMATRIX, _ 
    World As D3DMATRIX)

Now we can get the 2D point, we need to know what to do with it, how we coordinate the rest of the data with a bounding box to tell if an area of 3D space is going to be visible. The following diagram will help explain all the possible situations:

Take the above representation of 9 bounding boxes, we're only interested in the vertices, not the lines - the lines are there just to make it easier to see. If we go through all of these cubes we can tell if they're in or out of the blue square, which represents the visible area of the screen (0-1024 and 0-768 for example), a cube is visible if any of the vertices is within the blue square - simple as that, a square is not visible if all of the vertices are outside the square. In the above diagram all but cube 7 are going to be partly visible. Unfortunately it's not going to be as simple as that, take the next diagram for example:

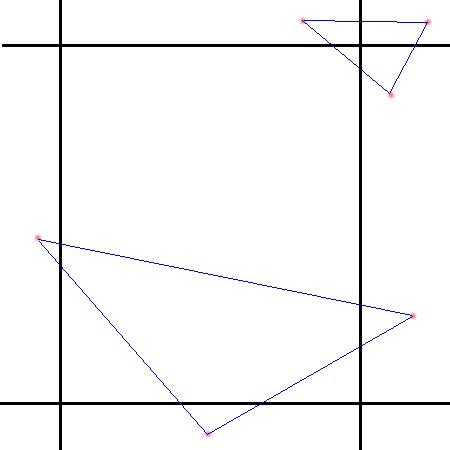
In this diagrame both of the triangles will of been rejected based on our previous rules - yet it's quite obvious that they are both going to be partly visible. To take this into account we need to know where off the screen the points are - are they to the left, to the right, above or below? only if all the vertices are to one of the extremes can we be certain that it's definately not a visible region. To sum things up the following list will be the rules for acceptance/rejection:

• if any of the vertices are within the screen area the box is PARTLY VISIBLE
• if all of the vertices are within the screen area the box is TOTALLY VISIBLE
• if all of the vertices are to a far extreme (up/down/left/right) then the box is TOTALLY INVISIBLE
• if all of the vertices are out of the screen area, but not in the same extreme the box is PARTLY VISIBLE
• if the above is true, but all the vertices are greater than the two adjacent extremes then the box is TOTALLY INVISIBLE

The above set of rules should work for 99.9% of cases, you may find the odd exception to the rule, if you do ammend the list and carry on...

We now want to generate a generic function that returns one of eight states, the reason for having lots of states will be seen later, where we need to know what sort of invisible we're talking about. The eight states are: Partly Visible, Totally Visible, Totally Invisible, To Screen Left, To Screen Right, To Screen Top, To Screen Bottom and To Screen Back. The code I've written for this is the following:

this function can then be extended to take a 3D box, representing an area of space - and check if that's visible or not, it is this code that required the greater detail of invisibility flags - this function would not work properly without them. The great power of this part is that you can rule out vast areas of 3D space with only 6 calculations, if the corners of the box are all invisible, every point inside will also be invisible...

We can now use these functions quite simply to render a tile (or not), the following code excerpt takes a 3D flat tile and checks it's visibility before rendering it:

simple really!

5. Tips and Tricks

Now that you have 3 techniques under your belt I'll discuss some further uses for these techniques, and a few other simple tricks for reducing the amount of geometry you need to render. The following list is by no means a definative guide - just a starter, you can look up these ideas further, or combine and alter them to fit whatever you want to do...

• LOD Algorithms. Level Of Detail algorithms can reduce the amount of geometry you need to render, or in the case of landscapes and wide open spaces can dramatically increase the visible distance. Think about it logically, the geometry in the distance will not be visible in quite the same detail as that in the foreground, so why render it in such a way. Reducing the texture detail and geometry density (vertex/triangle count) will allow you to draw things further away without using up large amounts of processing time. LOD algorithms can be quite complicated, but there are several good articles around.
• Invisible Geometry. This is more likely to be a thing that you'll add to your level editor rather than do it in realtime. If you have your view locked to a certain position or have it restricted to certain areas then use this to your advantage - dont draw, or even consider drawing parts of a world that will never be visible. A good example of this would be the tops of mountains - if the camera will never get up high enough to see the top of a mountain there's no point even creating the mountain top - let alone checking it for visibility every frame. The same can go for rooms in a first-person environment, if the level designer puts a room, or some geometry that can never be seen by the camera/player remove it. Determining if a piece of geometry will be visible could be extremely difficult - so this method may or may not suit your game engine.
• Unlit/dark geometry. Take the first person example again, if an entire room is unlit and completely dark in some cases you could get away without drawing any of it! this only works if there isn't anything behind that will become visible (sky/other parts of the level).
• Bounding Box sectors. This was mentioned briefly in the projection culling section. If you have your level divided into large, regular sections, or you can design your world to be - testing against the bounding box of this area will let you know if the entire area is visible/invisible - in either case you know that there is no need to visibility-test anything inside the box as it's either all visible or all invisible. It gets a little more tricky when only part of the box is visible.
• Quadtrees. These are an extremely popular technique for landscape engines and extend the bounding box theory. This algorithm can reduce the number of visibility tests by 80% in some cases, meaning that whilst not drawing any excess geometry you also reduce the number of calculations done to achieve this. There is a good article on www.gamedev.net about this.
• BSP (Binary Space Partions) Tree. These tend to always be mentioned in terms of first person shooters, but they can be used for other game types as well. The principle behind them is very similiar to that of a quadtree. Check out GameDev.net or Gamasutra.com for articles about this technique

techniques do not need to be limited by anything in this article, designing a custom method that suits your game will often be much better than trying to twist your game to fit another algorithm. If you are at the planning stage of a game then designing the world to suit one of these algorithms could be a good idea though...

Hopefully you now have all of the information required to get started on optimising the rendering part of your game. Several of the ideas in section 5 could have been covered here, but it would have made for a massive article so I decided against it - in favour of pointing you to better dedicated articles.

As usual you can download the complete source from the top of the page.