|
Dijkstra's
Path Finding Algorithm
Author
:
Jack Hoxley
Written : 26th January 2001
Contact : [Web]
[Email]
Download : GM_Dijkstra.Zip
[62 Kb]
Contents
of this lesson:
1. Introduction
2. The Problem
3. Solving it using a graph
4. The Data Structures
5. Dijkstra's Algorithm
6. Making this work in code
7. Enhancing the Algorithm
1.
Introduction
Path
finding is a crucial part of almost every game, and has been for a very long
time. Take your average strategy game - Red Alert for example - select a unit
and click somewhere on the map, off the unit goes until it gets to the location
- how did it get there, why didn't it get stuck anywhere? The reason being that
it used a path finding algorithm of some kind. Even games like Quake/Unreal
use path finding - your character may not, but how does the enemy get from A
to B?
There
are many forms of path finding, graph based, natural, bump 'n' grind, tracing,
orbital... each subset with many different implementations, or complete hybrids
of both. Depending on the type of game and the players view point, selecting
a good path finding algorithm is essential - an RTS game using the bump 'n'
grind method (where it drives into a wall, changes angle a bit, drives into
the wall, changes angle again - until it gets around the object) would look
awful - the player would be able to watch his crack, highly trained army tanks
driving into rocks and trees quicker than a learner driver... Natural algorithms
(modelling genetics) are by far the best type of algorithm for path finding
- for looks anyway; they simulate (theoretically) how our minds solve the problem
of path finding; but unfortunately they aren't really a realistic option just
yet - they require vast amounts of memory and quite a bit of processing power
- which isn't good for the current set of computer hardware available.
By
the end of this article you will be able to construct, with ease, a path finding
module for your game - lightning quick and very simple as well. This algorithm
can traverse a fairly simple map in a fraction of a millisecond - anything from
1/10000th to 1/1000000th of a second - which is pretty damn fast. After we have
our path, all we need to do is follow it...
2.
The Problem
Take
a blank map - just a flat terrain, choose a point A and B, to get from A to
B you just follow a vector between the two - not too complicate really. Introduce
something as simple as a tree in this landscape and it gets a whole lot more
complicated - if the line between AB is blocked by the tree we either have to
walk through it or walk around it - which isn't too difficult in this case,
just sidestep, go around and get back on course again. Introduce a more complicated
set of obstacles - caves, paths, forests, cliffs, buildings - and it gets even
more complicated; so complicated that you probably wouldn't be able to get to
where you want to without getting stuck somewhere. Take this picture for example...
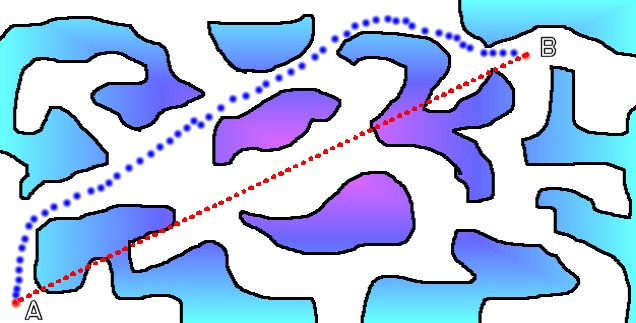
On
the above picture you can see two paths - "As the Crow flies" and
"As the Crow Walks", assuming that the unit cannot actually fly over
the obstructions you can instantly see the problem with the straight (red) line
method. Instead we would have to take the blue line - and walk around and between
the various obsticles on our route.
So,
to put it simply, the problem is - how do we mathematically (and programmatically)
calculate a path from A to B in a similiar style to the blue line?
3.
Solving it using a graph
Now
we've outlined the problem we can start thinking about how to solve it. The
easiest, fastest and most realistic looking method is by using graphs. Not graphs
like bar-charts and line-graphs that you may be used to - network graphs. The
following illustration will explain:
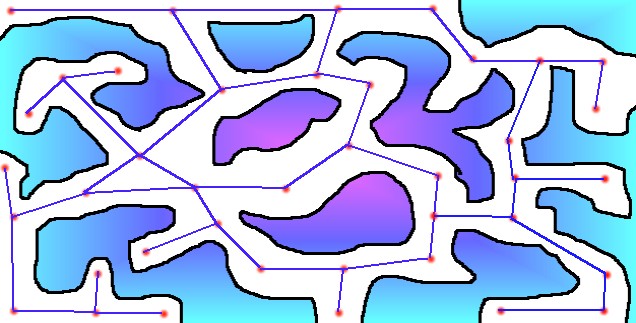
The
blue lines and red dots are the graph, and as you can see they extend to almost
every place on the map. A bit of terminology for you: The red dots are vertices
(plural of vertex) and the blue, connecting, lines are called edges. Some people
call them nodes and arcs, but they all mean the same thing.
To
construct a graph the first thing we need to do is place the vertices, these
should be key points that extend into all the little nooks and crannies of our
world, this example uses 40 of them, but you can quite easily go into the hundreds
before it starts to slow down to much. The key point to remember when placing
these vertices is NOT to put them too close together, and not put them too far
apart. Each vertex needs to be able to "see" another vertex along
a straight line, in order to do this you may need to add additional vertices
to the world. The order that they are placed in doesn't really matter a great
deal - but some sort of logical pattern will help slightly later on.
The
next step will be to work out where the edges go, if you take a quick look at
the above illustration you'll see that each vertex has at most 4 edges coming
out of it, and that all edges have a start and end vertex. I've programmed the
algorithm to only use 4 possible routes from one vertex purely because of processing
power, as we'll see later on the algorithm needs to analyse each vertex connected
to the current vertex before it'll move on - having 100 possible edges coming
from one vertex will quite obviously cause a slow down; should you need more
than this you can easily increase it to 5 or 6, but many more than that and
it might start slowing down.

Just
a little bit more complicated now, as I said before, a logical pattern to numbering
is quite useful - in this case it tends to go left-right and back again. With
this information we can now construct our edges, we know what vertices there
are, we know how to identify them (through the number). Visually we can tell
that vertex 17 connects to vertices 10,12,20 and 21 - if we store this information
we can draw a line between vertex 17 and all the vertices it connects to. Do
this for every vertex on the map and we have ourselves a graph. This part will
almost certainly be done by a level designer pre-runtime and then saved out;
it would be fairly slow to generate them at runtime; and anyway - you fancy
writing an algorithm that designs a graph for the level? I didn't think so...
4.
The Data Structures
Now
we get onto the fun part, writing the code to hold all this data. At first glance
it looks fairly simple, but there are several ways in which it can go wrong
(I tried a few methods before getting one that I liked). The data that we need
to store can be contained in two UDT's :
'//Basic 2D Point structure
Private Type NodePoint
X As Long
Y As Long
End Type
Private Const nNodes As Long = 40
Dim NodeList(0 To nNodes - 1) As NodePoint
'//A structure that connects everything up
Private Type TreeNode
CurrNode As Long '//Pointer to an entry in the NodePoint Structure
NextNode(0 To 3) As Long '//Pointer to 4 attached nodes
Dist(0 To 3) As Double '//The weight of the edge CurrNode -> NextNode(n)
End Type
Dim TreeNodeList(0 To nNodes - 1) As TreeNode |
|
|
|
Not
too complicated really, but some explaining is required. The type NodePoint
could probably be integrated into the TreeNode structure, but I prefer it this
way around, makes things slightly easier I think. First we create an array of
nodes based on the constant nNodes (40 in this case), this array represents
the red dots on the diagrams above. Next we create a TreeNode structure, this
acts as a set of extended information on the red dots, where each node connects
and how far. The CurrNode member points to an entry in the NodeList( ) array,
so if we want to find the actual coordinates of the point we could use something
like:
NodeList(TreeNodeList(n).CurrNode).X
, NodeList(TreeNodeList(n).CurrNode).Y
and
if we wanted to look at a node that this one connects to we can analyse the
the NextNode( ) property:
TreeNodeList(TreeNodeList(n).NextNode(0)).CurrNode
Which
will query the node connected to the current node n for which NodePoint
it's using.
Lastly
we create an array of these tree nodes the same size as the number of actual
nodes there are - effectively saying, one tree node per node. You may well think
that some nodes, on the very edge of the graph, dont need a TreeNode structure
- that's wrong. If we know how to get there we also need to know how to get
back, when we're sitting on this node we'll have no information about any other
nodes that we can get to - even though we just travelled here. In general each
node will reference the one it's come from and the one it's going to - so that
we can go back and forth around the graph quite easily...
Filling
these structure is quite easy, the sample code (and this article) wont go into
how you can load/save the data, or let the user decide where the nodes are,
all of it is hardcoded into the Form_Load procedure. This should be avoided
at all costs for a proper game, but for this example it really doesn't matter
a great deal. It looks like this though:
NodeList(0).X
= 10
NodeList(0).Y
= 10
NodeList(1).X
= 175
NodeList(1).Y
= 10
NodeList(2).X
= 340
NodeList(2).Y
= 10
NodeList(3).X
= 430
NodeList(3).Y
= 10
NodeList(4).X
= 470
NodeList(4).Y
= 60
...
TreeNodeList(0).CurrNode = 0
TreeNodeList(0).NextNode(0)
= 1
TreeNodeList(0).NextNode(1)
= -1
TreeNodeList(0).NextNode(2)
= -1
TreeNodeList(0).NextNode(3)
= -1
TreeNodeList(1).CurrNode
= 1
TreeNodeList(1).NextNode(0)
= 0
TreeNodeList(1).NextNode(1)
= 2
TreeNodeList(1).NextNode(2)
= 11
TreeNodeList(1).NextNode(3)
= -1
TreeNodeList(2).CurrNode
= 2
TreeNodeList(2).NextNode(0)
= 1
TreeNodeList(2).NextNode(1)
= 3
TreeNodeList(2).NextNode(2)
= 12
TreeNodeList(2).NextNode(3)
= -1 |
|
|
|
The
only thing to note about this is the inclusion of -1 in the NextNode( ) properties.
As explained, the NextNode( ) member points to an entry in it's own array -
therefore it must be a + real number and within the array boundaries - which
makes -1 an error (you dont have a -1 entry in an array). Later on we'll be
including logic that ignores any NextNode( ) entries with a value of -1, which
will signify that there is no node to go to from there, which if you think about
it is perfectly reasonable, not every node should have or need 4 subsequent
edges coming out of it...
Lastly
we need to fill in the Dist( ) members, the reason that these are included will
become clear later on, but the calculation for getting the distance between
two points isn't as fast as I'd like, so pre-calculating it is preferable. So
after we've filled out all the data structures we need to run a loop through
all the TreeNodeList( ) entries calculating the distance between it and the
connected node. The code for doing this looks like:
Dim
I As
Long
For I
= 0 To
nNodes
- 1
If Not
(TreeNodeList(I).NextNode(0)
= -1)
Then
TreeNodeList(I).Dist(0)
= _
GetDist2D(NodeList(TreeNodeList(I).CurrNode).X,
NodeList(TreeNodeList(I).CurrNode).Y,
_
NodeList(TreeNodeList(I).NextNode(0)).X,
NodeList(TreeNodeList(I).NextNode(0)).Y)
If Not
(TreeNodeList(I).NextNode(1)
= -1)
Then
TreeNodeList(I).Dist(1)
= _
GetDist2D(NodeList(TreeNodeList(I).CurrNode).X,
NodeList(TreeNodeList(I).CurrNode).Y,
_
NodeList(TreeNodeList(I).NextNode(1)).X,
NodeList(TreeNodeList(I).NextNode(1)).Y)
If Not
(TreeNodeList(I).NextNode(2)
= -1)
Then
TreeNodeList(I).Dist(2)
= _
GetDist2D(NodeList(TreeNodeList(I).CurrNode).X,
NodeList(TreeNodeList(I).CurrNode).Y,
_
NodeList(TreeNodeList(I).NextNode(2)).X,
NodeList(TreeNodeList(I).NextNode(2)).Y)
If Not
(TreeNodeList(I).NextNode(3)
= -1)
Then
TreeNodeList(I).Dist(3)
= _
GetDist2D(NodeList(TreeNodeList(I).CurrNode).X,
NodeList(TreeNodeList(I).CurrNode).Y,
_
NodeList(TreeNodeList(I).NextNode(3)).X,
NodeList(TreeNodeList(I).NextNode(3)).Y)
Next I
'//The above code uses this function for calculating the distance:
Private
Function
GetDist2D(X
As
Long,
Y As
Long,
X1 As
Long,
Y1 As
Long)
As
Long
GetDist2D
=
Sqr(((X
- X1)
^ 2) +
((Y -
Y1) ^
2))
End
Function |
|
|
|
Looks
quite complicated doesn't it - well it isn't. The GetDist2D( ) call is so long
partly because of the long names of variables I've used and partly because it
requires 4 parameters. Also note the precursor to each calculation: If Not
(TreeNodeList(I).NextNode(0) = -1) Then which basically says "If the
next node is anything other than -1 we'll calculate the distance", as mentioned
above, -1 indicates that the branch does not go anywhere.
5.
Dijkstra's Algorithm
In
1959 Dijkstra designed an algorithm to solve such a problem. Take a series of
vertices interconnected by edges, each edge has a weight (in this case the distance)
and we know the start vertex and the end vertex.
Before
we begin to think about making some code for this algorithm we need to understand
how it works, which fortunately is very simple - I picked it up in 15 minutes
from my maths book. First I'll explain the stages required to find the path,
then I'll run through a simple mathmatical example:
Step
0: Preparation
We're going to be doing several calculations and needing to store numbers. These
can be setup in the following table:
| Vertex Number |
Visit Number |
Distance |
Temporary |
| |
|
|
|
Step
1: Draw out the graph
Quite obviously we're going to need to have the graph drawn out in front of
us. Draw out the table as well with all the vertex numbers in place, but the
rest blank.
Step
2: Label the start vertex with Distance 0, Visit Number 1 and leave temporary
blank.
Step
3: Update the temporary variable
Choose all vertices that are connected to the current vertex and work out
the temporary variable by adding the distance in the current node to the distance
along the edge to the next node. Place this number in the temporary box ONLY
if it is lower than any existing value - if there's nothing there then this
will become the first one. We only calculate the temporary value if the vertex
DOESN'T have a vist number of distance number.
Step
4: Choose the next vertex to visit
Look through all the vertices in our list, pick the vertex with the lowest
temporary value that HASN'T been visited (it doesn't have a visit number of
distance value). If there are multiple-identical lowest values you can take
your pick. Increment the visit number by one (where the first vertex was 1,
we'll go up 2, 3, 4, 5 etc...), and copy the temporary value to the distance
box.
Step
5: Repeat
Repeat steps 3 and 4 until the destination vertex has been given a visit number
and a distance.
Step
6: Work out the path
The distance value on the destination vertex will be the shortest route from
source-destination. But the actual path isn't as simple as reading back through
the visit numbers (9, 8, 7, 6, 5...). We have to run another loop through
to find the shortest path. It is as simple as this: If vertex A lies on the
route then vertex B is the previous vertex if Distance at A - Distance at
B = Distance of edge AB. So we scan through all the visited vertices connected
to the destination and find which is the correct one, then we scan all visited
vertices connected to that vertex for the correct one, then again and again
until we reach the place we started from. The list of values we have will
be a route from End to Start, all we need to do is reverse this and we have
a path going from Start - Finish along the shortest possible route.
Simple
really. If your still scratching your head I'll run through a simple example
for you.
Take
the following graph network, okay, you can probably calculate the shortest route
easily, but we want to do it using Dijkstra's algorithm.
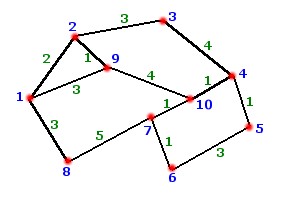
Task:
Find the shortest route from 1 to 5, where the black lines are edges, red dots
are vertices, blue numbers are vertex numbers and the green dots are the distances
(made up) along the edge.
Step
0 & 2: Draw our table, and add the first vertex
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
|
|
|
|
3
|
|
|
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
|
|
8
|
|
|
|
|
9
|
|
|
|
|
10
|
|
|
|
Step
3 ( i ) : Vertices 2, 8 and 9 can be reached from vertex 1, we need to work
out their temporary variables and add them to the table:
Vertex 2 Temp = 0 + 2 = 2
Vertex 8 Temp = 0 + 3 = 3
Vertex 9 Temp = 0 + 3 = 3
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
|
|
2
|
|
3
|
|
|
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
|
|
8
|
|
|
3
|
|
9
|
|
|
3
|
|
10
|
|
|
|
Step
4 ( i ) : Choose the lowest temporary value from all the unvisited vertices.
In this case it will be 2. We move here.
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
|
|
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
|
|
8
|
|
|
3
|
|
9
|
|
|
3
|
|
10
|
|
|
|
Step
3 ( ii ) : Vertices 1, 3 and 9 can be reached from vertex 2. Vertex 1
has already been visited so we ignore that one. Calculate the temporary variables
for vertices 3 and 9.
Vertex 3 = 2 + 3 = 5
Vertex 9 = 2 + 1 = 3
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
|
|
5
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
|
|
8
|
|
|
3
|
|
9
|
|
|
3
|
|
10
|
|
|
|
Step
4 ( ii ) : Choose the lowest temporary value from all the unvisted vertices,
we have a choice this time: 8 or 9. I'm going to Choose vertex 9 - as it'll
probably get us there quicker.
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
|
|
5
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
|
|
8
|
|
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
|
|
|
Step
3 ( iii ) : Vertices 1, 2 and 10 can all be reached from vertex 9. Calculate
their temporary variables and update the table.
Vertex 10 = 3 + 4 = 7
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
|
|
5
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
|
|
8
|
|
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
|
|
7
|
Step
4 ( iii ) : Choose the lowest temporary variable from all unvisited vertices.
In this case it's vertex 8, with a value of 3. Update our table:
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
|
|
5
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
|
|
8
|
4
|
3
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
|
|
7
|
Step
3 ( iv ) : Vertices 1 and 7 can be reached from vertex 8, having already
visited vertex 1 we only need to calculate a temporary value for vertex 7.
Vertex 7 = 3 + 5 = 8
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
|
|
5
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
8
|
|
8
|
4
|
3
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
|
|
7
|
Step
4 ( iv ) : Choose the lowest temporary value, which in this case is vertex
3 with temporary value 5.
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
5
|
5
|
5
|
|
4
|
|
|
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
8
|
|
8
|
4
|
3
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
|
|
7
|
Step
3 ( v ) : Vertices 2 and 4 can be visited from vertex 3, having already
visited vertex 2 we can ignore it and only calculate vertex 4.
Vertex 4 = 5 + 4 = 9
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
5
|
5
|
5
|
|
4
|
|
|
9
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
8
|
|
8
|
4
|
3
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
|
|
7
|
Step
4 ( v ) : Choose the lowest value, in this instance it's going to be vertex
10 with a temporary value of 7.
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
5
|
5
|
5
|
|
4
|
|
|
9
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
8
|
|
8
|
4
|
3
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
6
|
7
|
7
|
Step
3 ( vi ) : Vertices 4, 7 and 9 can be reached from vertex 10, having already
visited vertex 9 we only need to calculate vertices 4 and 7, both of which
already have a temporary value (so we may not need to replace it).
Vertex 4 = 7 + 1 = 8
Vertex 7 = 7 + 1 = 8
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
5
|
5
|
5
|
|
4
|
|
|
8
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
|
|
8
|
|
8
|
4
|
3
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
6
|
7
|
7
|
Step
4 ( vi ) : Choose the lowest temporary value of any unvisited vertex.
The only two we can choose from are 4 and 7, both of which have the same value.
I'm going to choose vertex 7 to goto next.
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
5
|
5
|
5
|
|
4
|
|
|
8
|
|
5
|
|
|
|
|
6
|
|
|
|
|
7
|
7
|
8
|
8
|
|
8
|
4
|
3
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
6
|
7
|
7
|
Step
3 ( vii ) : Vertices 8 and 6 can be visited from vertex 7, vertex 8 having
already been visited leaves only vertex 6 to be calculated.
Vertex 6 = 8 + 1 = 9
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
5
|
5
|
5
|
|
4
|
|
|
8
|
|
5
|
|
|
|
|
6
|
|
|
9
|
|
7
|
7
|
8
|
8
|
|
8
|
4
|
3
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
6
|
7
|
7
|
Step
4 ( vii ) : Choose the lowest temporary value (getting bored yet. I am)
- vertex 4 with a value of 8.
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
5
|
5
|
5
|
|
4
|
8
|
8
|
8
|
|
5
|
|
|
|
|
6
|
|
|
9
|
|
7
|
7
|
8
|
8
|
|
8
|
4
|
3
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
6
|
7
|
7
|
Step
3 ( viii ) : Vertices 3, 5 and 10 can be visited from vertex 4, vertex
3 and 10 have already been visited, so we only need to calculate vertex 5.
Vertex 5 = 8 + 1 = 9
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
5
|
5
|
5
|
|
4
|
8
|
8
|
8
|
|
5
|
|
|
9
|
|
6
|
|
|
|
|
7
|
7
|
8
|
8
|
|
8
|
4
|
3
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
6
|
7
|
7
|
Step
4 ( viii ) : Oh look, we're at the destination - vertex 5. No more calculating
required, just fill in the visit number and distance.
|
Vertex
Number
|
Visit
Number
|
Distance
|
Temporary
|
|
1
|
1
|
0
|
0
|
|
2
|
2
|
2
|
2
|
|
3
|
5
|
5
|
5
|
|
4
|
8
|
8
|
8
|
|
5
|
9
|
9
|
9
|
|
6
|
|
|
|
|
7
|
7
|
8
|
8
|
|
8
|
4
|
3
|
3
|
|
9
|
3
|
3
|
3
|
|
10
|
6
|
7
|
7
|
Finally
we've completed the first part of the search. On larger networks you'll very
rarely visit such a high proportion of the vertices (90% here), but as it
was quite small we've only not visited vertex 6. It's useful to note that
it took us only 8 iterations to collect all the information, even if we quadruple
this number a computer will make easy work of this algorithm.
The
last part - deciphering the data so that we're left with a path from vertex
1 to 5 isn't too difficult, and goes like this:
Vertex
5 Distance - Vertex 4 Distance = 9 - 8 = 1
Vertex 5 Distance - Vertex 6 Distance = Cant do, didn't visit vertex 6
So
the next vertex back from the destination is 4, path is currently 5-4
Vertex
4 Distance - Vertex 10 Distance = 8 - 7 = 1 'Correct, same as edge length
Vertex 4 Distance - Vertex 3 Distance = 8 - 5 = 3 'Incorrect, edge length
is 4
So
vertex 10 is the next one back, path is currently 5-4-10
Vertex
10 Distance - Vertex 7 Distance = 7 - 8 = -1 'Definately not correct
Vertex 10 Distance - Vertex 9 Distance = 7 - 3 = 4 'Correct route
Vertex
9 is on the route home as well then, path is currently 5-4-10-9
Vertex
9 Distance - Vertex 2 Distance = 3 - 2 = 1
Vertex 9 Distance - Vertex 1 Distance = 3 - 0 = 3
Now
this is a funny one, both vertices can be on the path, but we'll choose vertex
1 - as it's the source vertex. But if we had of chosen vertex 2 instead we'd
still get home, just not on the most direct route (from vertex 9 it's 3 units
both ways back to node 1). I hadn't actually planned for this to happen, and
we're lucky that both ways still yield a valid result. As you'll see in the
sample code (you can download it above) I've included a bench mark tool that
checks if the graph is a complete graph (a mathematical term for a graph where
from every vertex you can get to every other vertex), and out of 10,000 attempts
on a 40 vertex graph it's never failed to find a path...
So
the final path from the finish to the start is 5-4-10-9-1 or 5-4-10-9-2-1,
but the first one uses less nodes... As you may well have noticed the path
is in the wrong direction, so if we reverse it, travelling from the start
(vertex 1) we take the route 9 to 10 to 4 to 5 (destination), which looks
like this:
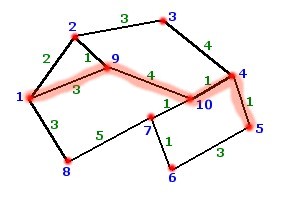
Which
if you think about it looks like the shortest and most direct route from vertex
1 to vertex 5.
6.
Making this work in code
As
you'll agree (I hope), it's much better to let the computer work out the path
for us - there's probably about 5 A4 pages of tables and workings in the previous
section - and for a relatively simple graph. Fancy calculating the path around
an office block? 1000's of nodes? didn't think so....
Also,
considering the fact that the computer would of done all the above work in under
1ms ....
Onto
the main feature then - converting this algorithm to visual basic code. We already
have the data structures setup (section 4), so all we really need to do is design
a function that takes a start and finish vertex index, and spits out a path
that we can follow from A to B.
The
first thing we need to do is update our TreeNode structure so that we can store
the table information. We also need to setup an open ended array where we can
dump the finalised path in. The updated structures look like:
'//A structure that connects everything up
Private Type TreeNode
CurrNode As Long '//Pointer to an entry in the NodePoint Structure
NextNode(0 To 3) As Long '//Pointer to 4 attached nodes
Dist(0 To 3) As Double '//The weight of
the arc CurrNode - NextNode(n)
'## DIJKSTRAs ALGORITHM ##
VisitNumber As Long '//What order was this node visited
Distance As Double '//What the current distance was at this point
TmpVar As Double '//Temporary area for storing distance data...
End Type
Dim nPathList As Long '//How many entries are in our path...
Dim PATHLIST() As Long |
|
|
|
Everything
else remains the same. Now we move onto the actual pathfinding code. Before
we start doing the proper searching we need to lay the ground work:
Private
Function
DijkstraPathFinding(NodeSrc
As
Long,
NodeDest
As
Long)
As
Boolean
'//0. Any variables required
Dim I
As
Long
Dim
bRunning
As
Boolean
Dim
CurrentVisitNumber
As
Long '//Which visit the current node will be
Dim
CurrNode
As
Long '//Which node we are scanning...
Dim
LowestNodeFound
As
Long '//For when we are searching for the lowest temporary value
Dim
LowestValFound
As
Double '//For above variable
If
NodeSrc
=
NodeDest
Then
'we're already there...
nPathList
= 2
ReDim
PATHLIST(2)
As
Long
PATHLIST(1)
=
NodeSrc
PATHLIST(2)
=
NodeDest
DijkstraPathFinding
= True
Exit
Function
End If
'//1. Setup all the data we need
For I
= 0 To
nNodes
- 1
TreeNodeList(I).VisitNumber
= -1 '//-1 indicates not visited
TreeNodeList(I).Distance
= -1 '//Unknown distance
TreeNodeList(I).TmpVar
=
99999 '//A high number that can easily be beaten
Next I
'//Set the first variable
TreeNodeList(NodeSrc).VisitNumber
= 1
CurrentVisitNumber
= 1 '//Initialise
CurrNode
=
NodeSrc
TreeNodeList(NodeSrc).Distance
= 0
TreeNodeList(NodeSrc).TmpVar
= 0 |
|
|
|
Above
is the function header, the variables that are required and the ground work
that needs to be done. The first stage is to check if where we're going is where
we're at - in this case it just returns a path starting and finishing in the
same place; hopefully the calling function will have checked this already (and
decide not to call the function). Next we run through each node setting some
default values for the table entries - in particular the .TmpVar value is set
very high, hopefully we wont get a graph where we're using edges 100,000 or
more in length (cant imagine what would really make use of something like that).
Then we do stage 2, make the source node the first visited with distance and
temporary variables of 0.
As
you've already seen, the Dijkstra algorithm comes in two parts, visiting and
marking the vertices and then tracing the route back. The first part of marking
the vertices is shown here. Note that it's effectively an infinite loop, whilst
it's unlikely to get stuck on a complete graph if you start modifying the algorithm
(see the next section) you could introduce states where the destination cannot
be reached - in this case the loop would never terminate. The next section uses
a time-out clause that breaks out after a certain time period if no path can
be found, if we dont have this the loop could continue for ever (or until windohs
crashes). If you think that your implementation will incur this scenario then
you should include a time-out clause in this loop as well.
Do
While
bRunning
=
False
'//2a. Go to each node that the current one touches
'and make it's temporary variable =
source distance + weight of the arc
If Not
(TreeNodeList(CurrNode).NextNode(0)
= -1)
Then
TreeNodeList(TreeNodeList(CurrNode).NextNode(0)).TmpVar
= _
MIN(TreeNodeList(CurrNode).Dist(0)
+
TreeNodeList(CurrNode).Distance,
_
TreeNodeList(TreeNodeList(CurrNode).NextNode(0)).TmpVar)
If Not
(TreeNodeList(CurrNode).NextNode(1)
= -1)
Then
TreeNodeList(TreeNodeList(CurrNode).NextNode(1)).TmpVar
= _
MIN(TreeNodeList(CurrNode).Dist(1)
+
TreeNodeList(CurrNode).Distance,
_
TreeNodeList(TreeNodeList(CurrNode).NextNode(1)).TmpVar)
If Not
(TreeNodeList(CurrNode).NextNode(2)
= -1)
Then
TreeNodeList(TreeNodeList(CurrNode).NextNode(2)).TmpVar
= _
MIN(TreeNodeList(CurrNode).Dist(2)
+
TreeNodeList(CurrNode).Distance,
_
TreeNodeList(TreeNodeList(CurrNode).NextNode(2)).TmpVar)
If Not
(TreeNodeList(CurrNode).NextNode(3)
= -1)
Then
TreeNodeList(TreeNodeList(CurrNode).NextNode(3)).TmpVar
= _
MIN(TreeNodeList(CurrNode).Dist(3)
+
TreeNodeList(CurrNode).Distance,
_
TreeNodeList(TreeNodeList(CurrNode).NextNode(3)).TmpVar)
'//2b. Decide which node has the lowest temporary variable (Free choice if multiple)
LowestValFound
=
100999 'Hopefully the graph isn't this big :)
For I
= 0 To
nNodes
- 1 '//If we have more than 1000-2000 nodes this part will be horribly slow...
If (TreeNodeList(I).TmpVar
<=
LowestValFound)
And (TreeNodeList(I).TmpVar
>=
0) And
_
(TreeNodeList(I).VisitNumber
<
0)
Then
'make
sure
we
ignore
the
-1's
and
visited
nodes
'We
have a
new
lowest
value
LowestValFound
=
TreeNodeList(I).TmpVar
LowestNodeFound
= I
End If
Next I
'**NB: If there are multiple lowest values then this method will choose the last one found...
'//2c. Mark this node with the next visit number and copy the tmpvar -> distance
CurrentVisitNumber
=
CurrentVisitNumber
+ 1
TreeNodeList(LowestNodeFound).VisitNumber
=
CurrentVisitNumber
TreeNodeList(LowestNodeFound).Distance
=
TreeNodeList(LowestNodeFound).TmpVar
CurrNode
=
LowestNodeFound '//Copy the variable for next time...
'//2d. If this node IS NOT the destination then go onto the next iteration...
If
CurrNode
=
NodeDest
Then
bRunning
= True '//We've gotten to the destination
Else
bRunning
=
False '//Still not there yet
End If
Loop
|
|
|
|
the
above is fairly explanatory, and identical to the worked example above. The
only reason it looks complicated is because of the large identifiers/names used
and the large number of logic statements that need to be evaluated.
The
next part of the function looks equally scary, but is actually very simple.
The core code is actually repeated 4 times for each of the possible child nodes,
so you only need to understand the first one and you'll understand all the others.
bRunning
=
False
CurrNode
=
NodeDest '//Start at the end, and work backwards...
Dim
lngTimeTaken
As
Long
lngTimeTaken
=
GetTickCount
nPathList
= 1
ReDim
PATHLIST(nPathList)
As
Long
PATHLIST(1)
=
NodeDest '//Put the first node in...
Do
While
bRunning
=
False
'//First we check that the current node isn't
actually the start
'because if it is then we've found the path already
If
CurrNode
=
NodeSrc
Then
bRunning
= True
GoTo
SkipToEnd:
ElseIf
GetTickCount
-
lngTimeTaken
>
1000
Then
'Break out if we haven't found a solution in under 1 second
bRunning
= True
DijkstraPathFinding
=
False
Exit
Function
GoTo
SkipToEnd:
End If
'//Scan through each node that we visited
If (TreeNodeList(CurrNode).NextNode(0)
>=
0)
Then '//Only if there is a node in this direction
If (TreeNodeList(TreeNodeList(CurrNode).NextNode(0)).VisitNumber
>=
0)
Then
'//Only
if we
visited
this
node...
If
TreeNodeList(CurrNode).Distance
-
TreeNodeList(TreeNodeList(CurrNode).NextNode(0)).Distance
= _
TreeNodeList(CurrNode).Dist(0)
Then
'NextNode(0) is part of the route home
nPathList
=
nPathList
+ 1
ReDim
Preserve
PATHLIST(nPathList)
As
Long
PATHLIST(nPathList)
=
TreeNodeList(CurrNode).NextNode(0)
CurrNode
=
TreeNodeList(CurrNode).NextNode(0)
GoTo
SkipToEnd:
End If
End If
End If
If (TreeNodeList(CurrNode).NextNode(1)
>=
0)
Then '//Only if there is a node in this direction
If (TreeNodeList(TreeNodeList(CurrNode).NextNode(1)).VisitNumber
>=
0)
Then
'//Only
if we
visited
this
node...
If
TreeNodeList(CurrNode).Distance
-
TreeNodeList(TreeNodeList(CurrNode).NextNode(1)).Distance
= _
TreeNodeList(CurrNode).Dist(1)
Then
'NextNode(1) is part of the route home
nPathList
=
nPathList
+ 1
ReDim
Preserve
PATHLIST(nPathList)
As
Long
PATHLIST(nPathList)
=
TreeNodeList(CurrNode).NextNode(1)
CurrNode
=
TreeNodeList(CurrNode).NextNode(1)
GoTo
SkipToEnd:
End If
End If
End If
If (TreeNodeList(CurrNode).NextNode(2)
>=
0)
Then '//Only if there is a node in this direction
If (TreeNodeList(TreeNodeList(CurrNode).NextNode(2)).VisitNumber
>=
0)
Then
'//Only
if we
visited
this
node...
If
TreeNodeList(CurrNode).Distance
-
TreeNodeList(TreeNodeList(CurrNode).NextNode(2)).Distance
=
_
TreeNodeList(CurrNode).Dist(2)
Then
'NextNode(2) is part of the route home
nPathList
=
nPathList
+ 1
ReDim
Preserve
PATHLIST(nPathList)
As
Long
PATHLIST(nPathList)
=
TreeNodeList(CurrNode).NextNode(2)
CurrNode
=
TreeNodeList(CurrNode).NextNode(2)
GoTo
SkipToEnd:
End If
End If
End If
If (TreeNodeList(CurrNode).NextNode(3)
>=
0)
Then '//Only if there is a node in this direction
If (TreeNodeList(TreeNodeList(CurrNode).NextNode(3)).VisitNumber
>=
0)
Then
'//Only
if we
visited
this
node...
If
TreeNodeList(CurrNode).Distance
-
TreeNodeList(TreeNodeList(CurrNode).NextNode(3)).Distance
= _
TreeNodeList(CurrNode).Dist(3)
Then
'NextNode(3) is part of the route home
nPathList
=
nPathList
+ 1
ReDim
Preserve
PATHLIST(nPathList)
As
Long
PATHLIST(nPathList)
=
TreeNodeList(CurrNode).NextNode(3)
CurrNode
=
TreeNodeList(CurrNode).NextNode(3)
GoTo
SkipToEnd:
End If
End If
End If
SkipToEnd:
Loop |
|
|
|
Looks
complicated doesn't it. After we've decided that the vertex is part of the path
we increase the size of the pathlist by 1 and add the entry in the new space,
before setting the current node to be the new path entry we found - and then
carrying on. If we get a situation (as in the worked example) where there are
two possible paths to take this code will take the first found, as you can see,
when it finds a valid vertex it skips straight to the end of the loop, so if
there is a valid vertex on NextNode(0) and NextNode(3) it'll evaluate (0) and
then skip straight to the end - it wont even look at (3).
The
final part of the code is to reverse the function, if you were really looking
to save time and speed up this algorithm (as if it isn't fast enough already)
you could remove this next part and read the array backwards - but I find it
easier to read it start-finish.
Dim
TmpArray()
As
Long
ReDim
TmpArray(nPathList)
As
Long
For I
=
nPathList
To 1
Step
-1
TmpArray(I)
=
PATHLIST(((nPathList
- I) +
1))
Next I
For I
= 1 To
nPathList
PATHLIST(I)
=
TmpArray(I)
Next I
DijkstraPathFinding
= True
End
Function |
|
|
|
Not
too complicated really, we create an array the same size as the path list, run
through the original array backwards copying the data in the correct order into
the temporary array, then we copy the temporary array back to the main array.
And then we've finished.
At
this point in time we have our path finding algorithm completed, if we feed
in two indices to nodes, and the relevent structures are filled out correctly
it'll fill out an array with the path to take - what more could you want? The
code in it's current form is extremely simple to adapt (see the next section)
and easy to implement into other projects - just copy the code and structures
across, fill them as you require and off you go....
7.
Enhancing the Algorithm
In
the final section of this mammoth article I want to discuss improvements and
alterations that you can make to this algorithm. Whilst it is a perfectly functional
algorithm and works 100% of the time on all properly created graphs there are
several things that I thought about changing - and it is quite possible you
have several adaptations you may want to add. Here's my list:
Edge
Weighting
Currently the "weight" of an edge is just the distance between it's
start and end vertex. This is fine, but what if we want to disuade the player
from going down one route - or in certain circumstances stop them going down
a route altogether. One example of this would be a landscape with a swamp and
a path. You're standing on one side of the swamp and you want to get across
to the other side, if you make a network that joins you directly to the destination,
but also goes around the swamp as well, it's almost garaunteed that the path
across the swamp will be shorter, therefore the chosen route; but in real life
it would be easier to walk around the swamp than walk through it. You could
decide on a weighting system so that any edge going over a swamp gets a weight
2x the distance, which will almost always make the Dijkstra algorithm choose
the path around the edge, even more so if you weighted that path with a 0.5x
multiplier. You could also include conditional logic for an edge, if the player
has wading boots let him/her use the path across the swamp, or if the player
is in a hurry / running away from something let him/her use the path across
the swamp.
Moving
the Player
This article as only covered finding a route from one point on the graph to
another. Unless you have a pointlessly complex graph 99% of the time the player
will not be standing on top of a node. Hopefully the player will be standing
quite close to one though - and if you scan the network to find the closest
node you can vector the player towards that node, then once on the graph you
can move them around using interpolation, then once at the end you can do the
reverse of getting onto the network. You may well want to set it up so that
the player has to choose a node within n distance of itself, otherwise
you may well get natural pathfinding problems just getting it to the network.
Take a couple of steps back and I mentioned interpolation - whats that then?
If you haven't heard of it before it's the process of blending a set of values
between the start and end values by a given amount. Use the formula (B * V)
+ A * (1.0 - V) for this, where A is the source, B is the destination and V
is the distance between on a 0.0 to 1.0 scale, where 0.0 is at A and 1.0 is
at B. In order to follow the path decide what the start vertex is and the end
vertex is, then frame-by-frame move between them, when you're at the destination
switch it so that the previous destination is now the start and the destination
is now the next vertex in the path list...
Path
Variation
You may also encounter the problem of predictabilty when using any graph based
algorithm, if the player can see a birds-eye view (as in Red Alert) he/she may
well be able to remember the exact route that the AI characters take (or their
own), in doing this it can look very unnatural or can lead to poor gameplay
(or advantages to the player). To combat this you could either make more could
make more complex graphs, but this wouldn't actually work, the algorithm would
still pick the same shortest path every time; alternatively when moving along
the path you could add or subtract a random amount from the start/finish nodes
- this way it wouldn't always end in the same place or start in the same place;
this would have to be carefully controlled - small variation in confined spaces,
large variation in wide open landscapes.
Beyond
linear
Currently the lines drawn between the nodes are always straight lines. If you
wanted to make it more natural you could use curved lines between the nodes
- but these would have to be closely checked in the editor - the whole point
is that the lines dont intersect with any un-passable objects, which is quite
likely to happen with curves when in confined areas. If you're using this method
with DirectX8 you can make use of the D3DXVec3Hermite or D3DXVec2Hermite to
do curved interpolation for you.
C/C++
DLL
Whilst not everyone can also program in C/C++ this algorithm would be very easy
to port to a C/C++ DLL for use in VB. Whilst it's already quite fast I haven't
tried it on networks with 1000's of vertices in them - if you do find it slows
down to much you may well want to consider this option.
Generating
the Graph
One very easy way of generating a graph network that I believe Half-Life uses
(and probably others as well), is to make the level editor only have to place
the vertices, the editor then runs through the 4 closest vertices and puts an
edge in - whilst checking if the edge intersects with any solid/impassable objects.
Whilst not entirely necessary, it does make it easier for the level designer.
Storing
the graph
As mentioned above, the graphs will probably be generated by an editor and saved,
rather than generated at runtime. Storing them using VB's binary file access
is extremely extremely simple. Use this code snippet to save all the data that
this example uses, and to load it again:
Open
FileName
For
Binary
Access
Write
As #32
Put
#32, ,
nNodes
Put
#32,
1,
NodeList
Put
#32,
1,
TreeNodeList
Close
#32
Open
FileName
For
Binary
Access
Read
As #33
Get
#33, ,
nNodes
ReDim
NodeList(0
to
nNodes
- 1)
as
Long
Get
#33,
1,
NodeList
ReDim
TreeNodeList(0
to
nNodes
-1) as
Long
Get
#33,
1,
TreeNodeList
Close
#33 |
|
|
|
You
could also save a matrix of possible routes, depending on your graph size it
would not be very big at all. In this example I've used 40 nodes, if each of
these nodes can visit 39 other nodes (40 including itself) then a simple 2D
array would be capable of holding all the possible paths. On average each path
appears to pass through 8 vertices, if these are stored as integers (2 bytes)
that would require 16 bytes per path stored; 40x40 is 1600 possible paths, which
if 16 bytes in length would add up to 25600 bytes, or 25kb - not a particularly
large file. This would then require that you never needed to search for a path
during the actual game - just look it up in our table; this is fine if the weights
of the edges never change - but as mentioned above you may well want to dynamically
affect the paths chosen, in which case this method would be useless. For your
information, a 100 vertex graph would require 156kb to be stored, maybe less
if compression was used.
Things
to bare in mind when designing the graph
There are several things that you should bare in mind when designing the graphs
for this algorithm, whilst writing the sample code for this I made a couple
of mistakes with the edges and it made areas of the graph inaccessable and certain
nodes could not be reached. To guarantee that you'll have no problems write
a test that checks if every node can be reached by every other node - similar
to the 2D lookup table mentioned above, if this is satisfied we call it a Complete
Graph. The other thing you need to bare in mind are cycles - or loops. If you
design your graph so that there are cycles in it you may well find in the odd
situation an area of the graph that once entered cannot be exited, or as far
as the algorithm is concerned a solution will not be found.
Directional
graphs
Something that I haven't covered yet are diagraphs - directional graphs. Currently,
as long as the vertices are connected we can travel both ways - from and to.
Whilst it's perfectly possible with the current code to design a graph like
this, you may well want to add an option so that you can only travel one way
along an edge. During the Dijkstra search you can add additional logic in the
same place as it checks if "NextNode(0) = -1". If you decide to add
this option you have to be aware of two potential problems - sinks and sources.
A sink is a vertex where all edges come into it, but none leave it, so once
your at that vertex you cant leave again, and with sources you cant get there
because all edges point away from it (the only way you can get there is if you
start there).
3D
graphs
The final thing I can think of is changing this so that it's in 3 dimensions,
which is actually so simple it hurts. Change the NodePoint structure to include
a Z value, then alter the GetDist2D to be GetDist3D and thats it - the algorithm
will adapt fine and carry on working as per normal.
Well
done, you've survived a mamoth 24 (A4) page article. If you liked this or found
it useful drop me an email at the address at the top of the page (if you can
be bothered to scroll up again). If you do you can pick up the source code while
you're there...
|

