General: Matrix Maths
Author: Jack Hoxley
Written: 12th July 2001
Contact: [EMail]

Contents of this lesson
1. Introduction
2. 2D Transformations
3. 3D Transformations

1. Introduction

I've had so many emails in recent months about the transformation of 2D and 3D geometry that I'm getting bored with it - so I thought, to answer the question for the final time, I'll write an article to explain the whole thing. This is that article...

Transformation consists of 3 things - rotating (spinning things around), scaling (making things bigger/smaller) and translation (moving things around). With 3D graphics Direct3D will do 99% of the work for you, however, along my travels I've found a way of going faster - if you do the matrix maths calculations yourself you can go just that little bit faster (2.5x faster), we're talking the difference between 0.0001ms and 0.00005ms here, but if you're rendering 500+ objects a frame (several 1000 a second), it could be worth the extra effort. It also looks much cleverer! (if you open-source your code).

Onwards and upwards...

2. 2D Transformations

This is the most useful part, using either DirectDraw (fully 2D) or Direct3D (quasi 2D) no transformations are done for you - you want to rotate, translate or scale something you're gonna have to do it yourself. The actual mathematical proof behind all of this is a little complicated, and to be honest - it really makes much difference why it works, all we want to know is how to make it work for us. Much of the pure maths is glossed over here, if you're interested in proofs or further explanations dig out your old maths books or go searching the web - much of the pure maths is too lengthy to explain here.

We're going to be using a mathematical technique known as matrix maths - the ideas behind matrices (plural of matrix) isn't too important, heck! I dont even know exactly how to use them - I just learnt what I need to know about them. Matrix maths allows us to do the transformations relatively quickly, and relatively simply as well - just what I like.

The basic structure is like this [X,Y] ---} [M] ---} [X',Y'] (one set of coordinates goes in, something happens, and a new set of coordinates come out). [M] is the transformation matrix, it may scale the coordinates, rotate them, translate them or some combination of the 3. The best part is that you can combine all 3 transformations into one matrix (more on that later).

Translation
This is probably the easiest of the 3, and thus we'll start here. A 2D translation matrix for what we want is a 3x3 grid of numbers (known as a 3x3 matrix). for a translation it looks like this:

a bit weird really, isn't it. in order to translate a point by this matrix we must multiply the point by the matrix. Now this isn't as simple as it sounds, it's not quite like normal multiplication, and it's an awful lot more complicated. if we refer to all of the elements in row-column notation (ie, yx) and the rows are i and columns j, to get the FINAL value for element <i,j> we multiply each element in the row i (of the source matrix) with each element in the column j (of the destination matrix), we then add all of these values together and that is our final value. scared? look at this following example and see if you can understand what happened:

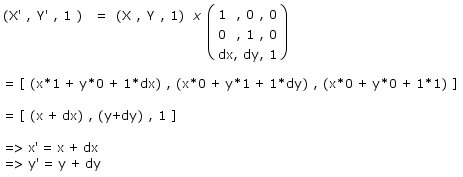
it aint too scary really, is it? the final results aren't particularly amazing - I'm pretty sure that without all this extra work you could of told me how to translate the original coordinates (the x' = x + dx part)... It'll come into it's own a little later on when we're combining rotation, scaling and translation into one big equation.

Rotation
Rotation is the big one - this is what everyone likes emailing me about. Rotating your sprite around is a very useful trick in games - and is often quite heavily used; therefore it obviously helps being able to do it! The following diagram shows you what the 2D rotation matrix should look like:

A little more scary this time - trig functions. The presence of these trig functions will bring the processing time for a rotation transformation up considerably - trig functions are slow. If you can optimise away any of the trig functions then do so - the only realistic optimisation to be done here is to pre-process CosX and SinX, as that will 1/2 the number of calls to Cos( ) or Sin( ). More on this later (when we do a bit of code).

I've already explained the basics of matrix multiplication in the translation section, so it should make sense this time around - if not, the derived equations are perfectly usable without any knowledge of matrix mathematics. Here's how we rotate our point [x,y] by X radians to retrieve [x',y'] :

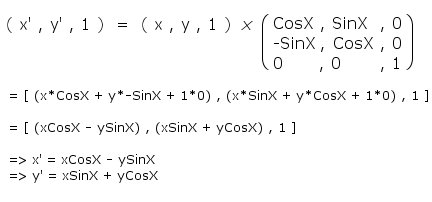
Again, not too simple if you can see your way through the matrix multiplication algorithm. Be careful to differentiate between the X and the x, the X is the angle (usually denoted as theta, q), and x is the coordinate.

Scaling
This isn't used as often, but it's pretty simple - so I may as well explain it, and we can incorporate it into the big matrix later on. You may have noticed that all of the matrices so far have had the r=c values equal to 1 (unless replaced by another value), this is because the r=c values are the scaling values - in previous matrices they are set to 1 so that they dont intefere with the resultant values. a matrix where all the values are 0 except the r=c values which are 1 is called the "identity matrix", which is a useful type of matrix, but not really relevant here.

Not at all complicated, and neither is the resulting equations - you can probably guess them now!

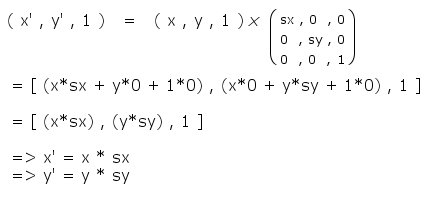
Tell me you could see that coming? it's pretty obvious...

Combining Transformations
Up till this point, the use of matrices has been a little pointless - the derived equations are enough to rotate, translate and scale. you could quite easily apply each transformation individually like this:

x' = x + dx
y' = y + dy

x'' = x'Cosq - y'Sinq
y'' = x'Sinq + y'Cosq

x''' = x'' * sx
y''' = y'' * sy

the above code would translate the point, rotate it around the origin and then scale it by a given factor - not necessarily what you want (rotation before translation is more common), but you can juggle the lines around. BUT, using matrices we can combine all 3 transformations together, then split them out into two lines - generating x',y' from x,y instead of going all the way to x''',y''' - is that not better?

The way we do this is by creating a master matrix - we multiply (using matrix multiplication) the translation, rotation and scaling matrices together into one matrix, then multiply the point x,y by this master matrix. A prior note on multiplication order - as with the 6 equations just listed it matter what order they go in, rotation-translation is very different from translation-rotation (one will create an orbiting body, the other will create a spinning object). Normally you would scale the points, rotate them and then translate them - but you'll need to decide which is best for your application. here is the complete proof for the "master matrix":

[M] is the Master Matrix
[S] is the scaling Matrix
[R] is the rotation Matrix
[T] is the translation Matrix

[M] = [S][R][T]
= ( [S]*[R] ) * [T]

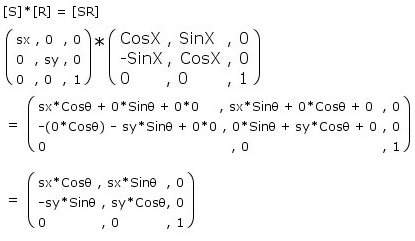
[M] = [SR][T]

there we have the final "Master Matrix". How amazing, if we now multiply a point [x,y,1] by this matrix we should be left with an equation to transform x and an equation to transform y - which will result in a rotation, translation and scaling. Arguably, through substitution, you could of combined the original 3 equations, but this way is open to much more powerful calculations - there are quite a few other types of transformation that can be done using matrices, and a few shortcuts can be found along the way as well. The following illustration indicates how the final all-in-one formula works:

So the final equation to transform the point (x,y) - rotating through q radians, scaling by (sx,sy) and translating by (dx,dy) units - is shown above. we can prove that this combined equation is actually correct by substituting in the previous set of equations - shown below.

Scale:
x' = x * sx
y' = y * sy

Rotate:
x'' = x'Cosq - y'Sinq
y'' = x'Sinq + y'Cosq

Translate:
x''' = x'' + dx
y''' = y'' + dy

Combined:
x' = ((x * sx)Cosq - (y * sy)Sinq) + dx
y' = ((x * sx)Sinq + (y * sy)Cosq) + dy

Simplified:
x' = xSxCosq - ySySinq + dx
y' = xSxSinq + ySyCosq + dy

and there, as if by magic - we've gotten the same formula back. The method you choose - by straight algebra or by matrix algebra - is your choice entirely; I personally prefer the matrix method as it allows for many 1000's of combinations; for example - scale, rotate, translate, rotate - will (given a flying saucer object) spin it around it's center and then spin it around the origin (like orbiting a planet) - you try doing that with those plain equations, it's still possible - but a little more complicated methinks. To finish things off, I've written a simple transformation function incorporating the overall equation.

Private Function Transform2DPoint(tX As Single, tY As Single, sX As Single, sY As Single, Theta As Single, SrcPt As Pt) As Pt
    '(tX,tY) describes the translation
    '(sX,sY) describes the scale
    'Theta describes the rotation
    'SrcPt is the point to be transformed
    '[RETURN] is the transformed point
    
    '   The general formulas:
    '   X' = xSxCosq - ySySinq + dx
    '   Y' = xSxSinq + ySyCosq + dy
    
    Dim Cosq As Single
    Dim Sinq As Single
    Cosq = Cos(Theta)
    Sinq = Sin(Theta)
    
    Transform2DPoint.X = (SrcPt.X * sX * Cosq) - (SrcPt.Y * sY * Sinq) + tX
    Transform2DPoint.Y = (SrcPt.X * sX * Sinq) + (SrcPt.Y * sY * Cosq) + tY
End Function

3. 3D Transformations

I'm not going to say much on this topic - 90% of what was in the previous section is still relevant in this section. More importantly, however, is that Direct3D (or any other 3D API) will do matrix transformations for you - only the specialist/elite will need to play around with the transformation matrices manually.

The advantage of having D3D do the actual transformation is that all you need to do is present the overall matrix and it'll work out what needs to happen - and in some cases the hardware will actually do the mathematics on the geometry (which is going to be 10000x faster than any software implementation). As visitors to the VoodooVB message board will be aware, I actually worked this out a while back and posted a generalised matrix formula for a 3D transformation. During my tests on this it gave exactly the same results as using the built in D3DX functions, yet was 1.6-2.6x faster than them. The only trade off is actually working out the generalised matrix in the first place - this usually only ever has to be done once.

The only two differences between the 2D matrices and the 3D matrices is their size (now 4x4 instead of 3x3) and there are 3 rotation matrices (x,y,z) - 2D rotation (on a plane) only requires you to have 1 rotation axis, 3D has 3 main rotation axis's...

The 5 matrices are shown below - this is for reference, given the information about 2D transformations you should quite easily be able to do some clever things with them...

- -

-

Finally, As I already mentioned, I calculated the generalised matrix for this a while back - and it's shown below.

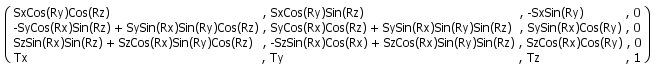
Pretty isn't it! Here's the same transformation matrix but in code:

Conclusion

Wow - that's a lot of maths, I sure hope someone out there finds all this useful!! either way, I'm sure the 2D-Transformation parts will be interesting for a lot of people. Enjoy!